The Woods of Woburn Sands & Aspley Heath
There is much on this website about the woods that surround the southern part of Woburn Sands, Aspley Guise and Aspley Heath. Dr. Williams of Aspley Guise believed they contributed to make unique atmospheric conditions in the area, which in turn made it ideal for TB patients to recover. This lead to investment by wealthy families who had ill relatives, and along with the coming of the railway and the general Victorian boom, meant that Woburn Sands and district grew and prospered. Day trippers came to “take the airs”, convalescent homes were built, postcards were made (thankfully!) and souvenirs were sold to tourists. Inns (and later guest houses) were filled, local services were needed, and it all added up to make the village a prosperous place.
But few people stop to wonder how the woods came to be. Surely they were just a natural feature?
Actually, most of the land around Aspley Heath, as the name suggests, was once open heath land. It wasn’t until the mid 1700’s that this changed and a huge quantity of trees was planted….
The following report is from Francis Moore of Aspley Guise. It was sent to the “Society for the Encouragement of Arts Manufactures and Commerce” (RSA) and was reprinted in their 1806 papers. It was Moore that organised the planting the trees that surround Aspley Heath now, and for doing so, he was awarded the RSA Gold Medal in 1779. Nearly 60,000 trees had been planted, and he says that “…I have now several hundred thousand of Scotch Fir plants raised by myself in my nursery beds which I shall plant out when of a proper age and season…”. Moore was one of the influential landowners in the area, and his house in Aspley Guise now bears his name, as the Moore Place Hotel.
The tables and map come from the original articles, while the postcard views used on this page are from the early 20th century.

From its foundation in 1754 until the 1850s, the main way in which the RSA encouraged the promotion of arts, manufactures and commerce was through its Premium Award Scheme. Premiums were advertised in six categories and cash or honorary awards were presented to prize-winning candidates.
By the 18th century natural supplies of timber, with which the country had once been richly endowed, were largely depleted. This was partly due to the use of wood as domestic fuel in industries such as iron-smelting, but also because the need to replace supplies had not been considered. Our naval power, which had become increasingly vital to the country, required a plentiful supply of timber for ship building, and so attention began to focus on the dwindling wood supply.
“To the Society for the Encouragement of Arts, Manufactures and Commerce
Gentlemen,
The perusal of your annual book wherein you offer premiums induced me to become a candidate for your favour and humbly to submit the following account of Plantations of Scotch Firs and the consequent improvement of barren and otherwise useless land to your attention.
I live in a part of England about forty miles distant from London where some of the land is exceedingly sandy poor and mountainous and totally unfit for cultivation at least the expence of cultivating it would cost infinitely more than the value of the land when cultivated so that many hundred acres now lie barren and apparently of no kind of use or benefit whatever such was the state of the land marked AC and D in the plans. (The original plans referred to are preserved in the Society’s Collection) Timber and fuel of all kinds being very dear (Coals 17d and 1s 6d per bushel Faggots £1 1s per hundred) and observing several small plantations of Scotch Firs to prosper very well upon this soil I was induced to make various plantations at different times and seasons for several years past and it is with the utmost pleasure I can assure you it has been attended with great success.
The plants are in a very flourishing condition many of which have made shoots of three feet and upwards within the year I am convinced by various instances and frequent observations in the neighbourhood of several small plantations of Scotch Firs of the respective growth of twelve sixteen twenty and twenty six years that being thinned at twelve sixteen and twenty years growth reducing the number of trees to one fourth or 676 trees there will remain a profit from the sale of the trees at the respective ages twelve sixteen and twenty years to defray every expence the planter has been put to with the clear profit of 676 trees per acre which at the age of twenty six years may be fairly computed to be of the value of 1s 6d per tree or nett profit £50 17s per acre besides the pleasing reflection of its being of the utmost utility to the poor by lessening the price of fuel the addition it makes to the beauty of the country and the certainty of lowering the price of timber and upon such a barren spot and soil as could not be turned to any other advantage or benefit whatever I am so thoroughly convinced of the good consequences attending this method of planting upon this soil that I have now several hundred thousand of Scotch Fir plants raised by myself in my nursery beds which I shall plant out when of a proper age and season.
Gentlemen, if this should meet with your approbation and encouragement it would add very much to the pleasure I have for many years experienced and be considered as the greatest honour conferred on.
Gentlemen with the greatest respect,
Your most humble servant
Francis Moore”
| By Plans annexed to the foregoing account it appears that: | Trees |
|---|---|
| 19 Acres were situated in the parish of Wavendon in the county of Bucks | 51,375 |
| 1 Acre In the parish of Aspley Guise in the county of Bedford | 2,704 |
| 1 Acre Wavendon in Bucks | 2,704 |
| 1 Acre In Aspley Guise in Bedfordshire | 2,704 |
| Total 22 acres | 59,488 |
NB A plan of that part of the above plantation which is situated in the parish of Wavendon and called Brown’s Wood along with a further description thereof will be found in the 23d Volume of the Society’s Transactions.
Fifteen years later in 1794, the trees had matured, and Moore showed some friends around his plantations, one of whom was Mr John Farey, of Aspley Guise. Moore made some comments about the profitability of his timber crop, and Farey was very interested.
John Farey (1766-1826) had shown aptitude in mathematics, drawing and surveying as a child, and in later life became an expert mineral surveyor. He was also a prolific author, who wrote on all manner of subjects, ranging from horticulture, geology, meteorology, metrology, currency decimalisation, music and mathematics to pacifism. He had been an agent for the Duke of Bedford since 1792.
The land the trees were on had by then been sold to the Duke of Bedford, and Farey engaged a local man, “…who then resided at Bowbrick hill, is named James Smith, a very steady and competent person…” to assist him in surveying the tree crop. With two local boys to help, they set about measuring a wide selection of the trees for height and width to work out how much profit could be made from a crop of timber. This was done by the great idea that Smith should “..take the circumference of each tree at the height of four feet from the ground, which height was readily ascertained by a particular button or mark on his waistcoat.”!

In 1802, the 5th Duke, Francis, died and was succeeded by his brother John. John brought in a new estate manager and Farey was replaced by Robert Salmon, but his work was recognised in 1805, when his report won him a Silver Medal from the RSA, the same society who had awarded Moore the Gold Medal for planting the trees in the first place.
The plantation he took special interest in is known as Browns Wood. This is not the new Milton Keynes estate, but an area of woodland that is still with us today. If you look to the left while driving out of Woburn Sands on the Bow Brickhill Road, Browns Wood is the trees about half way to Bow Brickhill.
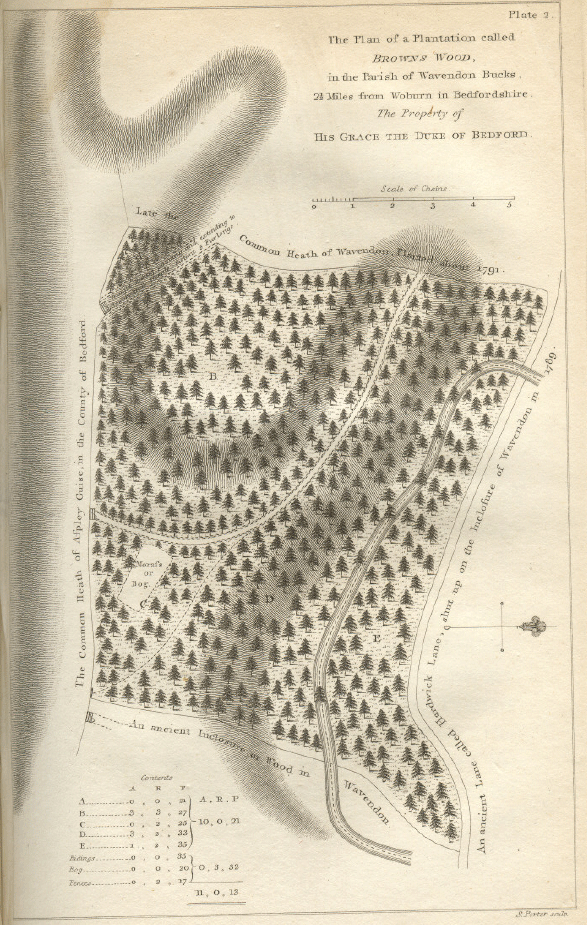
The map that accompanies the letters is reproduced here:
Farey’s letters are reported in the RSA Transactions for 1805:
The Silver Medal of the Society was this Session voted to Mr John Farey, No 12 Upper Crown Street, Westminster for Experiments on the Growth of Timber Trees. The following Communications were received from him.
A Plan of the Plantation referred to, called Brown’s Wood, is hereunto annexed and is the plantation described as 19 acres in the First Volume of the Society’s Transactions p 133.
Sir,
In the year 1778, Mr Francis Moore, of Aspley Guise, in Bedfordshire planted four pieces of sandy land with Scotch and a few other fir plants plans of which were laid before the Society of Arts &c with certificates in the usual form and the Gold Medal adjudged to Mr Moore for these Plantations Accounts thereof are preserved in the First Volume of the Society’s Transactions. Several circumstances concurred in the year 1794 to induce me with the approbation of the late Duke of Bedford to whom two of these plantations then belonged to have all the trees growing in one of the plantations in Wavendon carefully counted measured and valued in order to determine by an accurate and large experiment the actual growth and improvement in this plantation at the distance of sixteen years from its being planted In order to deduce several different averages a new and very accurate plan of this plantation was made and of five several parts into which it was divided.
Conceiving that these particulars may prove interesting and useful to gentlemen concerned in planting or who wish to make calculations on such improvements I have drawn out a detailed account of these operations with remarks referring to a plan of this plantation which I beg to submit to the consideration of the Society in hope that they will give the same a place in their next Volume of Transactions together with a re measurement of one of those divisions of the plantation to record the progress of the trees therein at twenty six years from their planting for which last particulars I am indebted to my friend Mr Robert Salmon of Woburn Park who will probably at a future period furnish you with further remarks of considerable utility on the progress and management of this and other young plantations.
I am Sir Your obedient servant
John Farey
12 Upper Crown Street Westminster
May 1st 1805
Reference to the ENGRAVING of the PLANTATION called Browns Wood in the parish of Wavendon Bucks with Mr Farey’s remarks thereon Set Plate II
Sir
Before entering on the measurement and other observations which I beg to have the honour of submitting to the Society of Arts relative to a plantation in Wavendon I beg leave to mention some circumstances which led to these inquiries on my part. I was one among a number of other persons of the neighbourhood of Aspley Guise a village on the western border of Bedfordshire whom Mr Francis Moore invited to meet him on the 8th of March 1794 to inspect his plantations and other improvements and I accordingly accompanied Mr Moore and five other gentlemen through several of the plantations which he had made it was particularly stated to us by Mr Moore while we were viewing a plantation of firs in Wavendon parish Bucks called Browns Wood that this was one among the plantations for which he was honoured with the gold medal in the year 1779 from your very excellent and useful Society. The particulars of the time of planting ages the plants &c he stated to us from a book then in his hands and shewed us five or six trees in Brown’s Wood which had been recently marked and numbered of which trees he stated the dimensions and value informing us that the same had been measured and ascertained a few days before by Mr Malcolm who was then collecting materials for his Report to the Board of Agriculture on the county of Buckingham.
From the terms of our invitation and the nature of Mr Moore’s conversation as we passed through his plantations I expected that he had some report prepared to be presented to your Society or to the Board of Agriculture on the progress and value of these plantations and to which he wished our certificates we separated however without any such thing being produced or mentioned but an idea was from that time imprinted strongly on my mind of the utility of periodical and accurate inspections to note the growth and increasing value of plantations like these especially of such whose planting has been recorded and honoured by the notice of so respectable a body as your Society. Soon after this Mr Malcolms Agricultural Report on the county of Bucks was published in which at pages 41 and 42 and 52 to 54 there is an account of this plantation and of your Society having honoured the owner with a gold medal and this determined me with the approbation of his Grace the Duke of Bedford to have all the trees in Brown’s Wood which then belonged to his Grace and was under my care carefully counted and measured and to keep thenceforward an exact account of all the thinnings or produce from it and to repeat the counting and measuring at intervals of eight or ten years or oftener. Although circumstances have prevented the full accomplishment of my intentions on this subject I hope that the following account of the measurements of the trees growing in this wood in 1794 may not be unacceptable to your Society and I have detailed the methods which I took from a hope it may stimulate others to furnish you with accurate and periodical measurements of the trees in some of the plantations whose origin has been stated in the volumes of your Transactions being convinced that much good would result from the publication at length of a number of such particular in ascertaining the best procedure in thinning and managing young plantations and of the comparative value of different kinds of trees besides furnishing accurate data or averages for estimating the value of other similar plantations without the great labour of measuring the whole
Having procured a measuring tape prepared with oil colours such as are now made by Mr Gary, optician, in the Strand, for measuring timber having inches on one side numbered on from one to ten, twenty, thirty &c without beginning again at the end of each foot its other side being divided into feet and quarters of feet having also provided a small tin kettle with a quantity of whiting and size prepared as for white washing and a painter’s brush, a book ruled from top to bottom into columns each about half an inch wide being also in readiness on the 15th of July 1794 I caused the measurement to be begun by a man and two boys. This man who then resided at Bowbrick hill is named James Smith, a very steady and competent person his business was to take the circumference of each tree at the height of four feet from the ground which height was readily ascertained by a particular button or mark on his waistcoat.

One of the boys constantly attended on one side of him with the book and as soon as he called out the inches which the tree girted wrote it down the other boy advancing on the other side immediately made a stroke of whiting around the tree about the place that had been measured this was for distinguishing those trees which had been measured.
On the second day I directed that such of the smaller trees as were found not to exceed four inches in circumference at four feet high should have their height measured instead of their circumference for which purpose the man held the ring of the tape to the extreme branch or leader of the tree and when this was above his reach using a stick with a hook or notch in its end to receive the ring of the tape to hold it up by while one of the boys stretched the tape to the ground and read off the feet which were regularly entered by the other boy one under another in the book along with the girts only distinguishing these by the letters ft after them this was done to prevent the trouble and risk of mistake in having different columns in use at the same time every alternate column was also left blank for room to note the kinds of trees except the Scotch firs of which the plantation principally consisted by the words Spruce Pine Larch &c after the girt. The planting in Brown’s Wood being divided by ridings or ditches into five distinct pieces in order to render the experiment more complete, I directed each one of these in succession to be completed and the accounts of each to be distinguished in the book I attended frequently to see that my orders were observed and in a few days the whole wood was got through the account extending to twenty pages of foolscap paper I now determined upon dividing the trees into classes according to their girts calling all those which girted five six seven eight &c inches at four feet high the fifth sixth seventh eighth &c classes and having prepared a sheet of paper with columns and room for the dimensions of five or six trees in each class on the 30th of July, I went to Brown’s Wood and Smith assisted me in measuring one hundred and eight trees which we performed with every regard to accuracy in four hours and a half.
Our method of selecting the trees was in walking through the wood in different directions to select a tree out of several others near it to which it appeared similar in growth and size the tree so selected was girted at four feet to refer it to its proper class and it was then measured by help of a ladder and a slight pole or rod to elevate the ring of the length tape to such a height in the tree as it could be used if cut down either for rafters of slight buildings for rails or for stakes in temporary fences &c in this I was governed by our custom of cutting off the top of the thinnings of this and similar plantations for sale. The tape being held I stretched it to the ground and read the feet from the black side thereof which I took down on the sheet of paper in the column for lengths under the proper class, Smith being at the same time upon the ladder without lowering or altering the position of the tape looked for the same figure on the red side of the tape which I had read and which was called put to him and level with or opposite thereto he found the proper girting place or middle of the length to be measured of the tree. After handing the pole down Smith took the circumference at that place with the tape first mentioned and read the inches which I wrote down against the length. The girt tapes also made by Gary are calculated to take the quarter girt at once which is great saving of time in measuring large timber but in an experiment on such small trees as these to avoid so many fractions it is better to use the inch tape.
The nearest foot in the heights and inch in the circumferences were set down rejecting or adding the fractional part when less than half a foot or inch and I made no allowance for the bark of the trees it not being usual with us to do so in selling similar fir trees to these from the thinning of plantations here I should remark that when Smith on the 15th of July began the girts of such trees as measured two three and four inches round at four feel high were set down but on considering next day the minuteness of the solid contents of such trees we went back and measured the extreme heights of several of these trees and found them to average seven nine and eleven feet respectively and after that the heights of such trees were set down as before mentioned instead of their girt such as were above six and a half and did not exceed eight feet in height were set down seven such as measured between eight and ten were set down nine and those between ten and twelve were set down eleven which is the reason that no eight and ten feet heights appear in the following abstracts In order that the Gentlemen of your Society may be able to judge how nearly I have obtained a correct average content of the trees in each class I have below copied the whole of the dimensions which were taken.
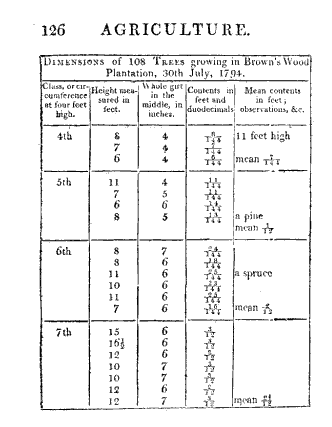
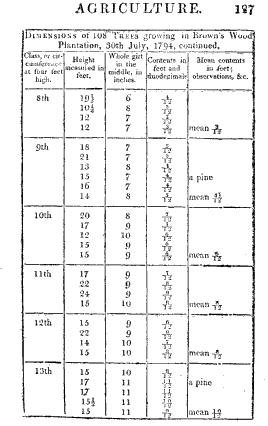
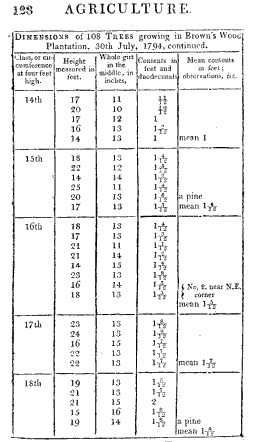
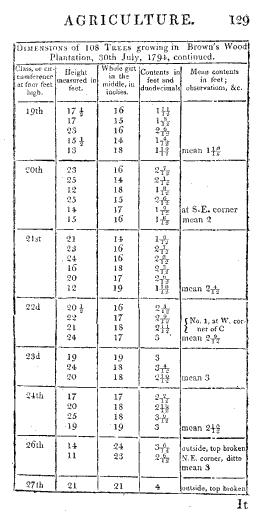
It may not be amiss to mention mode of calculation when the circumference is taken in inches instead of the one fourth girt to which the tables and slide rule in use are adapted viz Square the girt or multiply it by itself multiply this by the feet in length and divide the product by 2304 (Because the girt is four times too much before squaring and 144 square inches make a foot therefore 4X4X144=2304 is the divisor for reducing to the customary or round measure. See a paper on this subject in Tilloch’s Phil Mag No 75 vol xix, page 213) the quotient is the Content thus in the first tree in the 20th class 16x16x23÷2304=2 with 1280 remaining and (1280 multiplied by 12)÷2304=7 the Contents therefore is 2 7/12 feet. The remaining business was done by Smith and my brother Benjamin Farey in my office at Woburn. The original book was first carefully looked over and all the figures which had ft against them were circled round with a pencil to distinguish them, so were the spruce. pine larch &c A paper was then ruled into upright columns about a quarter of an inch wide and on the top the classes 5th 6th 7th 8th &c were written a person then read over the girt of the Scotch firs while another marked with a pencil each time under the proper class in this way they proceeded till a page of the original book was got through or till they had come to the end of one of the five divisions of the wood the number of marks under each class were then counted and set down under each other regularly in like manner the small Scotch firs of 1, 2, 3, 4, &co feet high were separately collected and set down under the proper classes.
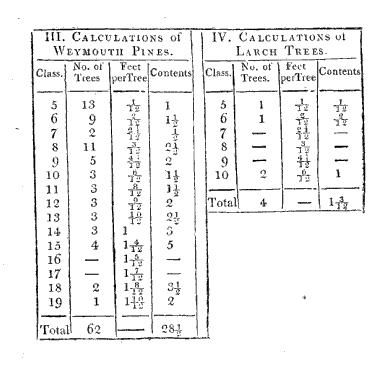
The trees of other kinds in that page were then collected into classes and the small ones arranged and added and the whole were added to the Scotch firs the total number of trees in that page of the original book was then counted, and if it did not agree with the collected total the whole was gone over again and thus each page was proved to be rightly collected. The above totals were then collected from each page on a sheet of paper, ruled, and entitled as in the following abstracts and the totals when collected for each division of the wood and kind of tree stood as in the folding pages opposite. The number of Scotch firs in the 5th 6th 7th &c classes were then collected in succession from each of these four abstracts, the same was done for the spruce Weymouth pines and larch and in order to ascertain the measure or cubic contents of the trees which had been measured in each class of the different kinds the four following Tables were drawn out. The numbers in the column entitled “Feet per Tree” being taken from the measurement of the trees before given
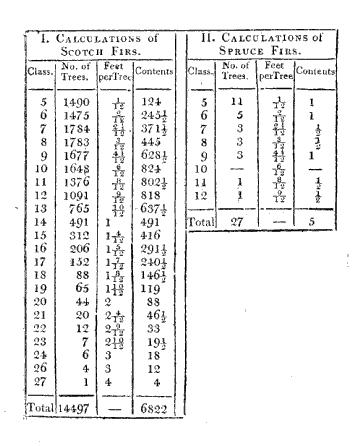
An Abstract of the Scotch Fir Trees which were growing in July 1794 on the small triangular part of Brown’s Wood containing 0A 0R 21P marked A on the plan annexed at the south west corner bounded on the south west by a fence against the common heath of Aspley in Bedfordshire on the north west by a fence against a young plantation of the Duke of Bedford’s in Wavendon and on the north east by the broad straight Riding which points to Bowbrick hill steeple.
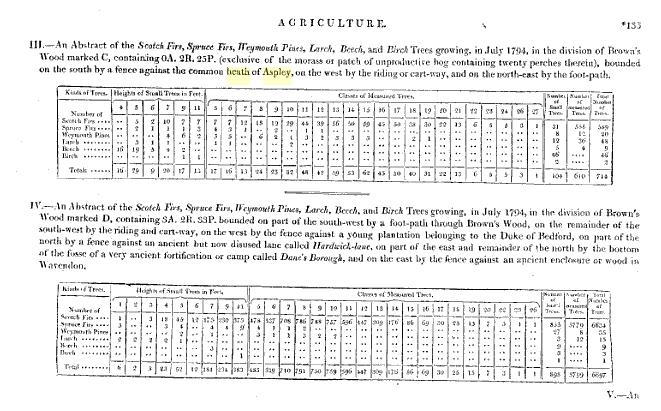
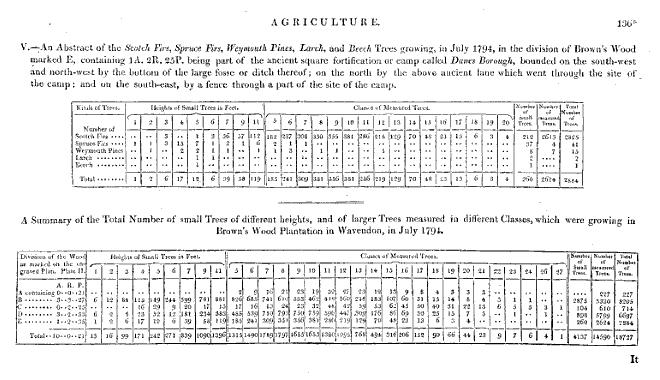
It appeared from consulting my accounts of the sales of a great number of lots of thinnings or poles from similar plantations that the average value of all the above measured trees was 12d per foot in the year 1794 and now probably the same are worth about 15d per foot. I also considered the value of the tops and lop or trimmings of the trees as nearly equal to the labour of cutting them down for sale and estimating the small trees at one penny each one with another the general account stood as follows viz
14497 Scotch firs measuring 6322 feet
27 Spruce do 5 do
62 Pines 28½ do
4 Larch 1½ do
14590 measured trees containing 6857 feet
at 12d are worth £342 17 0
4137 small trees from 1 to 11 feet high at 1d each £17 4 9
18727 trees in all £360 1 9
From whence it appears that the total value of the trees in this plantation in the year 1794 was about £360; that the average value of the whole number of trees was something above four pence three farthings each which is rather more than the value of each tree in the 9th class. If a mean tree as to measure be sought among all those which were measured as above it will be found to fall between the 11th and 12th classes.

If a mean tree be selected by regarding numbers only that is that there shall be as many measured trees larger than the mean as there are smaller than it this tree will be found in the 8th class. Brown’s Wood is situate near the northern edge of a thick stratum of red sand about 70 or 80 feet thick resting upon a stratum of blue clay or marl which lies, I believe, but seven feet below the division C in the plan and is the occasion of the springs and bog in the midst thereof the north west corner of D and a considerable part of B at its western end are upon the top of this thick stratum of sand which is in that part of it cemented into thin layers of sand stone by the oxydation of the large portion of iron which it contains and is on that account very poor and barren. Descending from these two barren points in all directions towards the bog and the vales one through the wood where the cart way goes up and the other on the south side of the wood the land grows better in quality not only as being more supplied with moisture but because the sand towards the middle and lower parts of this thick stratum are much better adapted to vegetation than the upper parts of it.
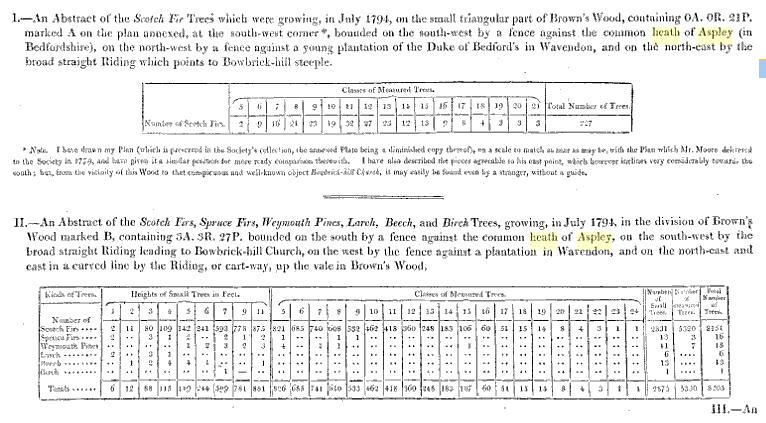
Previous to the new planting of this wood in 1778 it bore a straggling crop of oak and some other sorts of under wood except the rocky parts which were covered with heath only It was a very ancient enclosure and never appears to have been pared by the poor for fuel as the common heaths adjoining have been and some of them now are. Since the whole of the planted ground is 10A 0R 21P and the Acre Rood and Perch contain 43560, 10890 and 272.25 feet respectively, we have 10×43560+21×272.25=441317.25 superficial feet the contents thereof which divided by 18727 the total number of trees gives 23.566 feet for the surface or space occupied by each tree. Now we may consider the whole ground as made up of 18727 little square plots each containing 23.566 feet and having a tree in the centre of each and by extracting the square root of 23.566 we have 4.855 or about 4 feet 10 inches for the side of each square or the mean distance of the trees from each other supposing them equally distributed throughout the whole wood but as this is not the case I have given the result of similar calculations on each separate division of the wood and of the whole including fences rides and bog in the following table and also added the result of a similar calculation upon the 19 acres and 51376 plants which this wood was in 1778 stated to contain.
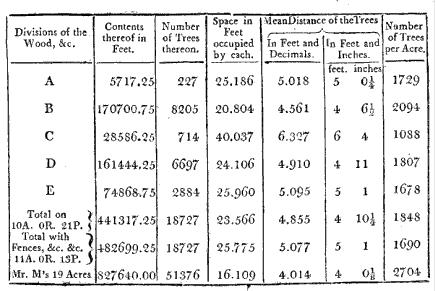
In considering the last column of the table it will appear that the division B has a much larger portion of plants per acre than the others have occasioned by the stunted and dwarf state of the plants upon the rocky parts above mentioned, indeed on about one third part of this division the plants had never been thinned or pruned and it was with considerable difficulty on account of the lateral branches that we got in among them to measure their heights their general distance asunder was found to be four feet and confirms this to have been the original distance of the plants in this wood before the thinnings commenced as in the last line of the above table and the certificates delivered in 1778 And as 2722 is the number of plants on an acre when set at four feet asunder and 10A 1R 36P or 456291 feet (including the rides and bog which were both planted at first I believe) was the quantity planted then say as 43560 the feet in an acre (456291): 2722: 28513 the number of trees at first planted by Mr Moore. The superior soil and situation of the division C occasioned the thinning thereof to be earlier begun and carried to a greater extent than in the other divisions as the trees increased in size and height which is the reason that this has the fewest plants per acre remaining. By referring back to the table containing the actual dimensions of 108 trees it will be found that the trees in the higher classes are much more irregular in their contents than the smaller trees are this arises from such trees as stood next the fence and were not drawn up to so great a height but spread more to branches than those within the wood and from such trees as had accidentally lost their leader or top both which had occasioned them to thicken more in the trunk and consequently they were placed in a higher class than their height and value justified; and this is a circumstance which future observers should particularly attend to as also in applying these dimensions to perfect trees of the same girt at four feet high within a plantation.
Here the number of trees altogether in those classes was so small that the error was of no material consequence. An inspection of the foregoing abstracts of the different divisions of this Wood will shew the superior growth of Scotch firs on this sandy soil above all the other sorts of trees especially when a few plants of different sorts are as in this case introduced among a large number of Scotch firs in a few years the latter overtop and at length shade completely most other kinds of trees and thus retard their growth if not entirely destroy them and there cannot I think remain a doubt with practical men but that plantations for profit should each be of one kind of tree except of deciduous trees where some are intended for timber and others for a permanent stub of underwood.
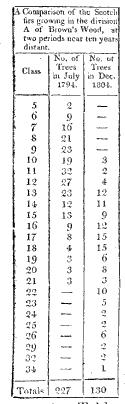
Mr Robert Salmon succeeded me on the death of the Duke of Bedford in the management of this and others of his Grace’s plantations and woods and through his kindness I am enabled to state the number of trees which remained growing in the small division A of Brown’s wood at Christmas 1804 and in order to shew the comparative number of trees in each class in 1794 and 1804 I have in the following table placed the particulars opposite each other.
By this Table it appears that the growth during the period mentioned and the various thinnings which took place therein and I lament that I am not able to give an account of the exact value of these thinnings had left none remaining of the classes below the 10th but had extended the classes from the 21st which was the largest tree in 1794 to the 34th the largest tree found among the 130 trees now remaining. By similar calculations to those in a foregoing Table it will be found that the mean distance of the trees in this division is now six feet seven inches and a half and the number of trees per acre 990 at twenty six years from the time of planting. I am not in possession of any exact accounts of the value of the thinnings from Brown’s Wood previous to or even for two or three years after Mr Moore sold the same to the Duke of Bedford but it will not I apprehend be much wide of the truth if we suppose the net produce of these thinnings previous to the measurement in 1794 to have repaid the original expense of clearing the ground and planting to have paid the composition in lieu of tithes to which it is subject and the parochial taxes together with the charges of looking after and repairing the fences thereof up to that time. And if we inquire by help of the tables of annuities or the rules of compound interest what annuity or rent forborne sixteen years allowing five per cent interest will amount to £360 we shall thus find that this plantation of 11a 0r 15p paid to the proprietor during the sixteen years previous to 1794 an annual rent of £15 4s 4d or at the rate of £1 7s 5d per acre per annum which must be considered as a very good rent for such land as this.
It was my intention to have given a rough calculation of the probable value of the trees now in Brown’s Wood founded on the supposition that the quality of the land in division A as adapted to the growth of fir trees and their consequent size number and management furnishes a fair average of the whole wood as I believe it to do but shall desist for the present from having compared the actual measurement of six trees therein in different classes which Mr Salmon lately sent me along with the number of trees and finding their contents particularly the larger ones so much to exceed that of trees in the same classes among the 108 trees which I measured in 1794 owing to the trees of my measuring being necessarily selected near the outside of the wood there being then none in the interior parts large enough and Mr Salmon’s trees of corresponding classes being selected from the inside of the wood and shall conclude with again calling the attention of future observers or calculators when deducing or using a mean measurement for different classes of trees to the above circumstances, and am Sir,
Your obedient servant
John Farey
12 Upper Crown Street, Westminster. May 1, 1805.
If you made it this far and have followed Farey and his calculations, well done! I am sure the profit involved meant complicated calculations like this were necessary, but I can’t imagine doing it all by hand…
My grateful thanks to the modern RSA for allowing me to reproduce the illustrations and letters on this page.
Page last updated Jan. 2019.
